[알고리즘] 소수 알고리즘

소수를 구하는 알고리즘을 알아보자.

 

소수의 정의를 이용한 방법

   N이 소수이면 2 ~ (N-1)로 나누어 떨어지지 않는다. 이 경우 2부터 N-1까지 연산이 필요하기 때문에 O(N)의 시간복잡도가 걸린다.

 

약수의 특징을 이용한 방법 

   N이 소수가 되려면, 2이상이고, N/2 이하의 자연수로 나누어 떨어지면 안된다. (N의 약수 중에서 가장 큰 것은 N/2보다 작거나 같다)

여전히 O(N)의 시간 복잡도를 갖는다.

 

약수의 특징을 이용한 방법2

   모든 수의 약수는 루트 N을 기준으로 대칭을 이룬다. 루트 N의 값 왼쪽에 있는 값을 기준으로 값 들을 조합해 대칭 오른쪽에 있는 수의 값을 구할 수 있다. O(루트 N)의 시간 복잡도를 가진다.

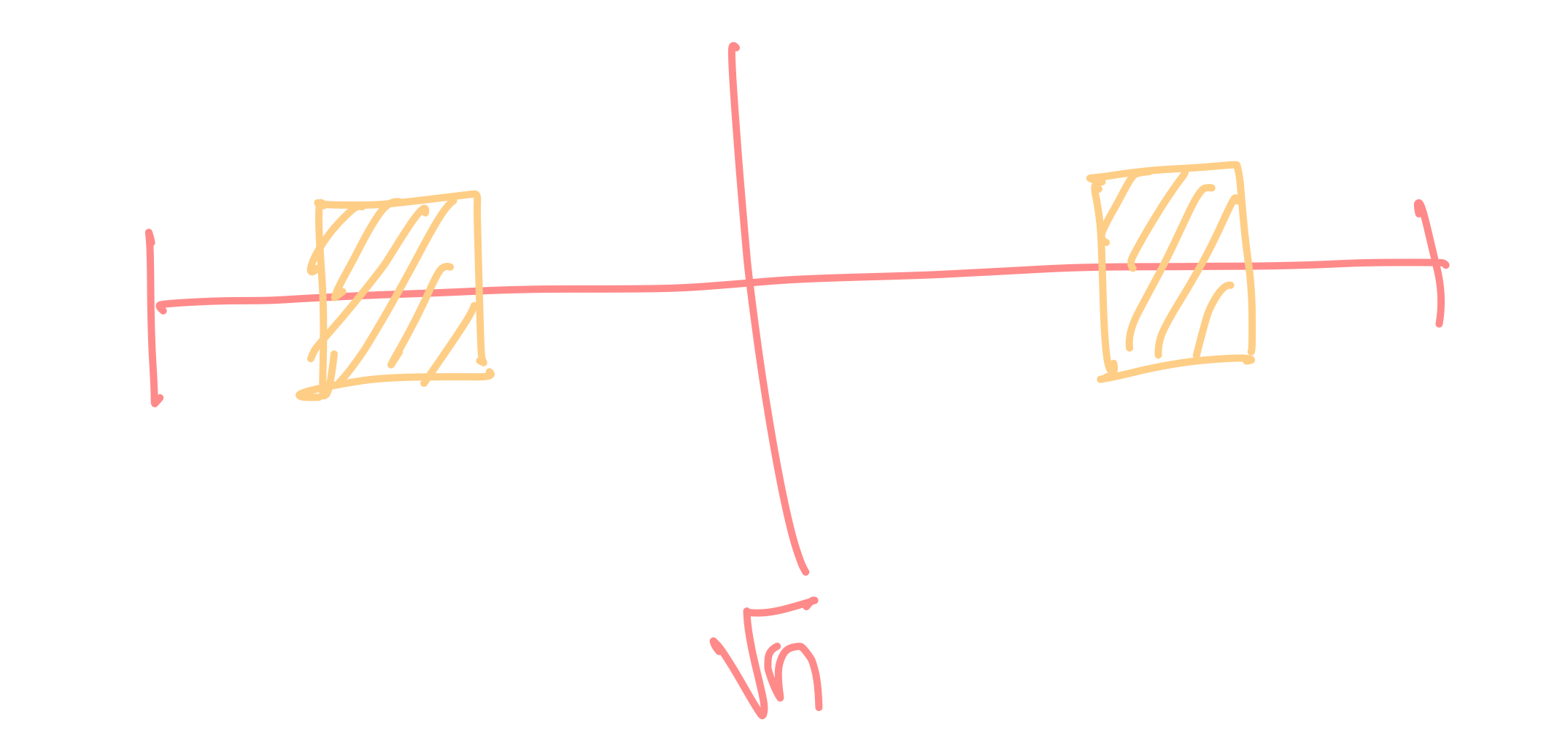
컴퓨터에서 실수는 근사값을 나타내기 때문에, 루트 N과 같은 경우는 다음 코드와 같이 i * i로 표기하는 것이 좋다.

public class B1978 {

    public static int answer = 0;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();
        while(n-- > 0) {
            int num = sc.nextInt();
            if(isPrime(num)) answer++;
        }

        System.out.println(answer);
    }

    public static boolean isPrime(int n) {
        if(n <= 1) {
            return false;
        }

        for(int i = 2; i * i <= n; i++) {
            if(n % i == 0) return false;
        }
        return true;
    }
}

 

에라토스테네스의 체

  https://brightmango.tistory.com/283?category=978023#toc-알고리즘%20설명 

[알고리즘] 소수 알고리즘(에스토스테네스 체)

 

 

관련 문제

https://www.acmicpc.net/problem/1929

1929번: 소수 구하기

https://www.acmicpc.net/problem/1978

1978번: 소수 찾기